

Estimation probabiliste de la taille des vues

Contrairement à l’estimation statistique des vues, l’estimation probabiliste ne présume rien quant à la nature des données. En contrepartie, l’estimation probabiliste requiert qu’on visite chaque élément dans l’ensemble initial afin d’en faire l’estimation. L’estimation probabiliste des vues fait appel au hachage des valeurs.
Notation hexadécimale
La notation hexadécimale est une façon de représenter les nombres en base 16. Les nombres de 0 à 15 sont 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Ensuite, 10 est la valeur 16, 11 est la valeur 17 et ainsi de suite.
Qu’est-ce que le hachage ?
Le hachage est une opération qui attribue à chaque valeur distincte un nombre (généralement aléatoire) [1] :
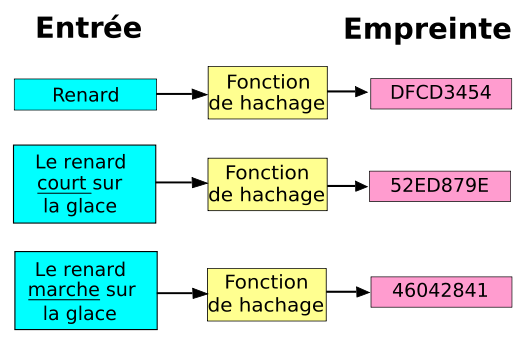
Dans une base de données, une fonction de hachage peut être construire avec une table qui associe un nombre à chaque valeur possible :
| valeur originale | valeur hachée |
| Renard | DFCD3454 |
| Le renard court sur la glace | 52ED879E |
| Le renard marche sur la glace | 46042841 |
Ainsi, la valeur Renard est toujours associée à la valeur hachée DFCD3454. Il n’est cependant pas nécessaire que la fonction de hachage soit injective, c’est-à-dire que deux valeurs peuvent partager la même valeur hachée. Il faut cependant qu’il s’agisse d’une fonction : à chaque valeur ne peut correspondre qu’une seule valeur hachée.
On utilise les fonctions de hachage en cryptographie et en recherche d’informations.
Qu’est-ce que le hachage uniforme ?
On dit qu’une famille de fonctions de hachage $ h$ est uniforme sur l’intervalle $ (0,2^L]$ si $ P(h(x)=y)=1/2^L$ pour toutes les valeurs $ x$. En somme, toutes les valeurs de hachage sont équiprobables.
Exemple. Soit la famille de fonctions de hachage suivante $ h(x)=c$ où $ c$ une valeur constante (indépendante de $ x$) choisie dans $ (0,2^L]$. Cette fonction de hachage est uniforme.
Qu’est-ce que le hachage universel ?
Comme le montre l’exemple précédent, une famille de fonctions de hachage uniforme peut être assez peu aléatoire. On dit qu’une famille de hachage est universelle sur l’intervalle $ (0,2^L]$ si $ P(h(x)=y \land h(x’)=y’)=1/4^L$ pour toutes les valeurs $ x, x’$ [2]. L’universalité assure une certaine indépendance entre les différentes valeurs hachées (une indépendance deux-à-deux). Le hachage universel implique le hachage uniforme.
De la même façon, on peut définir une condition plus forte encore. Si nous avons que $ P(h(x)=y \land h(x’)=y’ \land h(x’’)=y’’)=1/8^L$, on dit que la famille de fonctions de hachage est indépendante trois-à-trois. L’indépendance trois-à-trois implique le hachage universel.
Lecture suggérée (en anglais) :
J. Lawrence Carter and Mark N. Wegman. 1977. Universal classes of hash functions. In Proceedings of the ninth annual ACM symposium on Theory of computing (STOC ’77). ACM, New York, NY, USA, 106-112.
Hachage universel dans les tables
On peut facilement construire un hachage qui est au moins universel (et, en fait, mieux qu’universel), si le nombre de valeurs possibles dans chaque colonne est relativement petit.
Nous avons $ c$ colonnes. Pour chaque colonne, on compose une table qui crée une association entre chaque valeur distincte et une valeur aléatoire, comme dans notre exemple du renard. On dit que cette famille de fonctions de hachage est indépendante, car il n’y a aucune dépendance entre les différentes valeurs et leurs valeurs de hachages. Notons $ h_i(x)$ la fonction de hachage de la colonne $ i$, nous avons alors le théorème suivant.
Théorème. Soit $ t$ un vecteur ayant $ c$ composantes $ t_1, t_2,\ldots, t_c$. Soit $ c$ famille de fonctions de hachage indépendantes sur chaque composante $ h_1, h_2, \ldots , h_c$, alors la famille de fonctions de hachage $ h_1(t_1) \otimes h_2 (t_2) \otimes \cdots \otimes h_c (t_c)$ [3] est indépendante trois-à-trois.
(On trouve la preuve dans Lemire et Kaser, 2009.)
Estimation probabiliste de la taille d’une vue
On continue à s’intéresser aux requêtes du type GROUP BY : « SELECT dim1, dim2 FROM table GROUP BY dim1, dim2 ». L’idée fondamentale est la suivante. On prend chaque élément de la table originale, en ne s’intéressant qu’aux dimensions sélectionnées (par ex. dim1 et dim2). On construit une fonction de hachage sur les dimensions en question en utilisant l’approche de la section précédente (hachage universel dans les tables). Puis on représente chaque valeur hachée comme étant un vecteur de bits (par ex. 001011) et on cherche la position du premier bit ayant pour valeur 1 (par ex. 3). On procède ainsi pour l’ensemble de la table en cherchant la valeur 1 qui est le plus loin à gauche.
Voici un exemple :
| valeurs hachées | position du premier bit 1 |
| 001011 | 3 |
| 101111 | 1 |
| 001001 | 3 |
| 000110 | 4 |
| 000010 | 5 |
Dans cet exemple, la valeur maximale est alors 5. Selon un résultat de Flajolet et Martin [4], on estime alors qu’il doit y avoir $ 2^5/0.77351\approx 41.4$ valeurs distinctes dans le group by correspondant. En somme, si $ A$ est la position du bit 1 le plus à droite dans toutes vos valeurs hachées, l’estimation de Flajolet et Martin est $ 2^A /0.77351$. (La valeur $ 0.77351$ a été dérivée par Flajolet et Martin et il faut la prendre comme une constante.)
Cette approche est un peu naïve, et des algorithmes un peu plus complexes vont donner de meilleurs résultats. Voir, par exemple, Aouiche et Lemire, 2007. Cependant, une fois qu’on a compris la version simple de l’algorithme de Flajolet et Martin, les autres algorithmes sont simples à mettre en oeuvre.
Lecture suggérée (en anglais) :
Flajolet et Martin, Probabilistic counting algorithms for database applications, 1985
[1] Dans cet exemple, les nombres sont représentés en mode hexadécimal.
[2] Le symbole $ \land$ est le et logique.
[3] Le symbole $ \otimes$ est le ou exclusif : $ 01011 \otimes 11010 = 10001$.
[4] Flajolet et Martin, Probabilistic counting algorithms for database applications, 1985

